数独程序
数独解题器(Java)
在不了解数独的逻辑技巧和数据结构的情况下,只通过数独的规则解题,最先想到的算法就是试错法,也叫做回溯法。
设计试错的策略,减少试错的步骤是回溯法的目的,本质还是递归。
唯一余数
根据数独的规则,一个格子的候选数只有一个的时候应该优先填入,然后移除关联单元内的候选数,这种显而易见的策略叫做唯一余数技巧,对应的英文技巧名为Naked Single.
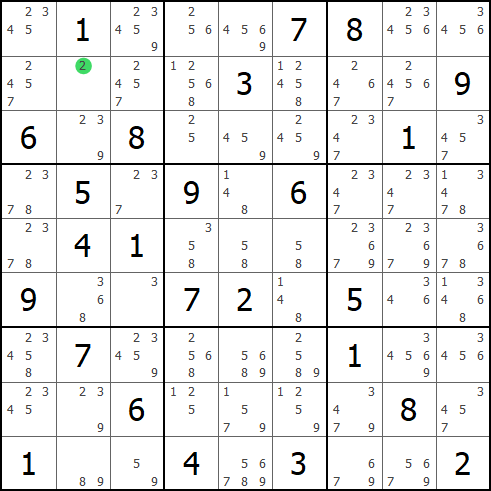
排除法
在一个单元区域内,某个数字只剩一个位置可填,也可以直接填入。通过行列宫排除就可以得到隐藏起来的可以直接填入的单个数字,这就是Hidden Single.
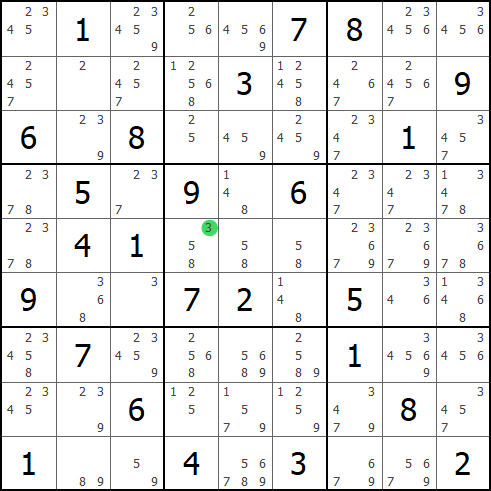
试错法
通过以上两种方式如果还不能进行下去,初学者又没有其他方法的时候就开始对某些多个候选数的单元格进行尝试填入,如果能进行到终盘则解开数独,如果出现矛盾,或者无数可填的格子,则回溯到第一个节点重新选择数字。显然这种策略需要找盘面上候选数尽量少的单元格开始,不过简单的题目可以奏效,困难的题目可能会导致指数级试错次数的增长。
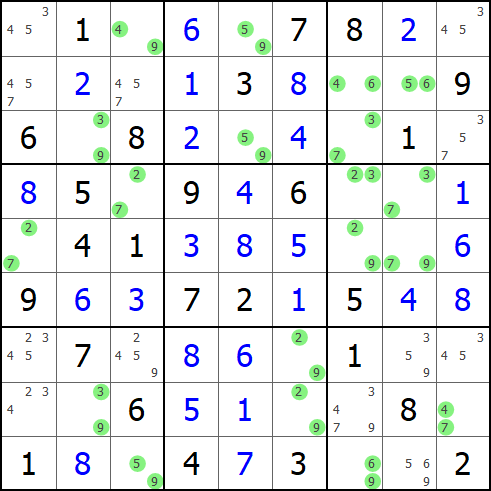
程序
通过Java编程实现数独解题器,不过这段使用回溯法没有考虑数独多解和无解的情况,所以继续优化。
package solver;
public class Test {
public static void main(String[] args) {
System.out.println(solveStandalone("000706002009002700400010090900050300030000008005870010700080400000600050090005000"));
}
/**
* 独立的数独求解函数,不依赖于类的其他部分
*
* @param puzzle 81个字符的字符串,'.' 或 '0' 表示空格,数字 '1'-'9' 表示已填数字
* @return 解决后的数独字符串,如果无解或多解则返回 null
*/
public static String solveStandalone(String puzzle) {
if (puzzle == null) {
return null;
}
// 找到第一个换行符的位置
int newlineIndex = puzzle.indexOf('\n');
// 如果没有换行符,则处理整个字符串;否则只处理到换行符为止
int endIndex = (newlineIndex == -1) ? puzzle.length() : newlineIndex;
// 取前81个字符或到换行符为止的字符(取较小值)
int processLength = Math.min(endIndex, 81);
// 如果有效字符不足81个,返回null
if (processLength < 81) {
return null;
}
// 将输入字符串转换为内部表示(整数数组)
int[] cells = new int[81];
for (int i = 0; i < 81; i++) {
char c = puzzle.charAt(i);
if (c >= '1' && c <= '9') {
cells[i] = c - '0';
} else {
cells[i] = 0;
}
}
// 使用回溯算法求解
int[] solution = solveSudoku(cells);
if (solution == null) {
return null;
}
// 将结果转换为字符串格式
StringBuilder result = new StringBuilder(81);
for (int i = 0; i < 81; i++) {
result.append((char) ('0' + solution[i]));
}
return result.toString();
}
/**
* 数独求解的核心实现
*
* @param cells 初始数独状态数组
* @return 解决后的数组,如果无解或多解则返回 null
*/
private static int[] solveSudoku(int[] cells) {
// 初始化候选值(位掩码表示)
int[] candidates = new int[81];
int[] solution = cells.clone();
int[] solutionCount = {0};
// 初始化所有位置的候选值
for (int i = 0; i < 81; i++) {
if (solution[i] == 0) {
candidates[i] = 0x1FF; // 9位都为1,代表1-9都可能
} else {
candidates[i] = 1 << (solution[i] - 1); // 只有对应位为1
}
}
// 应用初始约束
for (int i = 0; i < 81; i++) {
if (solution[i] != 0) {
if (!applyConstraints(candidates, solution, i, solution[i])) {
return null; // 初始状态就无效
}
}
}
// 应用基础约束(设置显性和隐性唯一候选数)
if (!setSingles(candidates, solution)) {
return null; // 初始状态就无效
}
// 检查是否已经解决
boolean isSolved = true;
for (int i = 0; i < 81; i++) {
if (solution[i] == 0) {
isSolved = false;
break;
}
}
if (isSolved) {
return solution;
}
// 使用回溯算法求解
return backtrack(candidates, solution, solutionCount);
}
/**
* 回溯算法核心实现
*/
private static int[] backtrack(int[] candidates, int[] solution, int[] solutionCounter) {
// 寻找候选数最少的空格
int index = -1;
int minCandidates = 10;
for (int i = 0; i < 81; i++) {
if (solution[i] == 0) {
int count = countBits(candidates[i]);
if (count < minCandidates) {
minCandidates = count;
index = i;
}
}
}
// 如果没有空格,说明已经解决
if (index == -1) {
solutionCounter[0]++;
if (solutionCounter[0] == 1) {
return solution.clone();
} else {
return null; // 多解情况
}
}
// 尝试该位置的每个候选值
int candidateValues = candidates[index];
for (int digit = 1; digit <= 9; digit++) {
if ((candidateValues & (1 << (digit - 1))) != 0) {
// 创建新的状态副本
int[] newCandidates = candidates.clone();
int[] newSolution = solution.clone();
// 设置当前数字
newSolution[index] = digit;
newCandidates[index] = 1 << (digit - 1);
// 传播约束
if (applyConstraints(newCandidates, newSolution, index, digit)) {
// 设置唯一候选数
if (setSingles(newCandidates, newSolution)) {
int[] result = backtrack(newCandidates, newSolution, solutionCounter);
if (result != null) {
if (solutionCounter[0] > 1) {
return null; // 多解
}
return result;
}
}
}
}
}
return null; // 无解
}
/**
* 应用约束传播
*/
private static boolean applyConstraints(int[] candidates, int[] solution, int index, int digit) {
int row = index / 9;
int col = index % 9;
int box = (row / 3) * 3 + (col / 3);
int mask = ~(1 << (digit - 1));
// 移除同行的候选数
for (int i = 0; i < 9; i++) {
int cellIndex = row * 9 + i;
if (cellIndex != index) {
candidates[cellIndex] &= mask;
}
}
// 移除同列的候选数
for (int i = 0; i < 9; i++) {
int cellIndex = i * 9 + col;
if (cellIndex != index) {
candidates[cellIndex] &= mask;
}
}
// 移除同宫的候选数
int boxRow = (box / 3) * 3;
int boxCol = (box % 3) * 3;
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
int cellIndex = (boxRow + i) * 9 + (boxCol + j);
if (cellIndex != index) {
candidates[cellIndex] &= mask;
}
}
}
// 检查是否有位置没有候选数且未填充
for (int i = 0; i < 81; i++) {
if (solution[i] == 0 && candidates[i] == 0) {
return false;
}
}
return true;
}
/**
* 设置所有唯一候选数(显性和隐性)
*/
private static boolean setSingles(int[] candidates, int[] solution) {
boolean changed;
do {
changed = false;
// 设置显性唯一候选数(Naked Singles)
for (int i = 0; i < 81; i++) {
if (solution[i] == 0 && countBits(candidates[i]) == 1) {
int digit = 1;
int temp = candidates[i];
while ((temp & 1) == 0) {
digit++;
temp >>= 1;
}
solution[i] = digit;
changed = true;
if (!applyConstraints(candidates, solution, i, digit)) {
return false;
}
}
}
// 检查行、列和宫中的隐性唯一候选数(Hidden Singles)
for (int digit = 1; digit <= 9; digit++) {
int mask = 1 << (digit - 1);
// 检查每行
for (int row = 0; row < 9; row++) {
int possiblePos = -1;
int count = 0;
for (int col = 0; col < 9; col++) {
int index = row * 9 + col;
if (solution[index] == 0 && (candidates[index] & mask) != 0) {
possiblePos = index;
count++;
}
}
if (count == 1) {
solution[possiblePos] = digit;
candidates[possiblePos] = mask;
changed = true;
if (!applyConstraints(candidates, solution, possiblePos, digit)) {
return false;
}
}
}
// 检查每列
for (int col = 0; col < 9; col++) {
int possiblePos = -1;
int count = 0;
for (int row = 0; row < 9; row++) {
int index = row * 9 + col;
if (solution[index] == 0 && (candidates[index] & mask) != 0) {
possiblePos = index;
count++;
}
}
if (count == 1) {
solution[possiblePos] = digit;
candidates[possiblePos] = mask;
changed = true;
if (!applyConstraints(candidates, solution, possiblePos, digit)) {
return false;
}
}
}
// 检查每个宫
for (int box = 0; box < 9; box++) {
int possiblePos = -1;
int count = 0;
int boxRow = (box / 3) * 3;
int boxCol = (box % 3) * 3;
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
int index = (boxRow + i) * 9 + (boxCol + j);
if (solution[index] == 0 && (candidates[index] & mask) != 0) {
possiblePos = index;
count++;
}
}
}
if (count == 1) {
solution[possiblePos] = digit;
candidates[possiblePos] = mask;
changed = true;
if (!applyConstraints(candidates, solution, possiblePos, digit)) {
return false;
}
}
}
}
} while (changed);
return true;
}
/**
* 计算整数中1的位数
*/
private static int countBits(int n) {
int count = 0;
while (n > 0) {
count += n & 1;
n >>= 1;
}
return count;
}
}使用枚举,判断多解、无解情况并记录盘面状态。
package generator;
public class Test {
// 定义求解结果状态枚举
public enum SolveResult {
SOLVED, // 唯一解
NO_SOLUTION, // 无解
MULTIPLE_SOLUTIONS // 多解
}
// 定义结果类来携带更多信息
public static class SudokuResult {
private final String solution;
private final SolveResult status;
public SudokuResult(String solution, SolveResult status) {
this.solution = solution;
this.status = status;
}
public String getSolution() {
return solution;
}
public SolveResult getStatus() {
return status;
}
@Override
public String toString() {
switch (status) {
case SOLVED:
return "唯一解:\n" + formatSolution(solution);
case NO_SOLUTION:
return "无解";
case MULTIPLE_SOLUTIONS:
return "多解";
default:
return "未知状态";
}
}
// 格式化数独解的显示
private String formatSolution(String solution) {
if (solution == null) return "";
StringBuilder formatted = new StringBuilder();
for (int i = 0; i < 9; i++) {
if (i > 0 && i % 3 == 0) {
formatted.append("------+-------+------\n");
}
for (int j = 0; j < 9; j++) {
if (j > 0 && j % 3 == 0) {
formatted.append("| ");
}
formatted.append(solution.charAt(i * 9 + j)).append(" ");
}
formatted.append("\n");
}
return formatted.toString();
}
}
public static void main(String[] args) {
// 测试唯一解情况
System.out.println(solveStandaloneWithDetails("000706002009002700400010090900050300030000008005870010700080400000600050090005000"));
// 测试无解情况
System.out.println("\n无解测试:");
System.out.println(solveStandaloneWithDetails("000776002009002700400010090900050300030000008005870010700080400000600050090005000"));
// 测试多解情况
System.out.println("\n多解测试:");
System.out.println(solveStandaloneWithDetails("000906002009002700400010090900050300030000008005870010700080400000600050090005000"));
}
/**
* 数独求解函数(增强版,返回详细结果)
*
* @param puzzle 81个字符的字符串,'.' 或 '0' 表示空格,数字 '1'-'9' 表示已填数字
* @return 包含解决结果和状态的SudokuResult对象
*/
public static SudokuResult solveStandaloneWithDetails(String puzzle) {
if (puzzle == null) {
return new SudokuResult(null, SolveResult.NO_SOLUTION);
}
// 找到第一个换行符的位置
int newlineIndex = puzzle.indexOf('\n');
// 如果没有换行符,则处理整个字符串;否则只处理到换行符为止
int endIndex = (newlineIndex == -1) ? puzzle.length() : newlineIndex;
// 取前81个字符或到换行符为止的字符(取较小值)
int processLength = Math.min(endIndex, 81);
// 如果有效字符不足81个,返回无解
if (processLength < 81) {
return new SudokuResult(null, SolveResult.NO_SOLUTION);
}
// 将输入字符串转换为内部表示(整数数组)
int[] cells = new int[81];
for (int i = 0; i < 81; i++) {
char c = puzzle.charAt(i);
if (c >= '1' && c <= '9') {
cells[i] = c - '0';
} else {
cells[i] = 0;
}
}
// 使用回溯算法求解
SolveInfo info = solveSudokuWithInfo(cells);
if (info.getStatus() == SolveResult.NO_SOLUTION) {
return new SudokuResult(null, SolveResult.NO_SOLUTION);
} else if (info.getStatus() == SolveResult.MULTIPLE_SOLUTIONS) {
return new SudokuResult(null, SolveResult.MULTIPLE_SOLUTIONS);
}
// 将结果转换为字符串格式
StringBuilder result = new StringBuilder(81);
for (int i = 0; i < 81; i++) {
result.append((char) ('0' + info.getSolution()[i]));
}
return new SudokuResult(result.toString(), SolveResult.SOLVED);
}
/**
* 数独求解函数(保持原有接口)
*
* @param puzzle 81个字符的字符串,'.' 或 '0' 表示空格,数字 '1'-'9' 表示已填数字
* @return 解决后的数独字符串,如果无解或多解则返回 null
*/
public static String solveStandalone(String puzzle) {
SudokuResult result = solveStandaloneWithDetails(puzzle);
return result.getSolution();
}
// 扩展的求解结果类
static class SolveInfo {
private final int[] solution;
private final SolveResult status;
public SolveInfo(int[] solution, SolveResult status) {
this.solution = solution;
this.status = status;
}
public int[] getSolution() {
return solution;
}
public SolveResult getStatus() {
return status;
}
}
/**
* 数独求解的核心实现(扩展版)
*
* @param cells 初始数独状态数组
* @return SolveInfo对象,包含解决结果和状态
*/
private static SolveInfo solveSudokuWithInfo(int[] cells) {
// 初始化候选值(位掩码表示)
int[] candidates = new int[81];
int[] solution = cells.clone();
// 初始化所有位置的候选值
for (int i = 0; i < 81; i++) {
if (solution[i] == 0) {
candidates[i] = 0x1FF; // 9位都为1,代表1-9都可能
} else {
candidates[i] = 1 << (solution[i] - 1); // 只有对应位为1
}
}
// 应用初始约束
for (int i = 0; i < 81; i++) {
if (solution[i] != 0) {
if (!applyConstraints(candidates, solution, i, solution[i])) {
return new SolveInfo(null, SolveResult.NO_SOLUTION); // 初始状态就无效
}
}
}
// 应用基础约束(设置显性和隐性唯一候选数)
if (!setSingles(candidates, solution)) {
return new SolveInfo(null, SolveResult.NO_SOLUTION); // 初始状态就无效
}
// 检查是否已经解决
boolean isSolved = true;
for (int i = 0; i < 81; i++) {
if (solution[i] == 0) {
isSolved = false;
break;
}
}
if (isSolved) {
return new SolveInfo(solution, SolveResult.SOLVED);
}
// 使用回溯算法求解
int[] solutionCount = {0};
int[] firstSolution = new int[81];
boolean hasFirstSolution = false;
// 创建用于回溯的候选值和解数组
int[] candidatesCopy = candidates.clone();
int[] solutionCopy = solution.clone();
backtrackWithInfo(candidatesCopy, solutionCopy, solutionCount, firstSolution, hasFirstSolution);
if (solutionCount[0] == 0) {
return new SolveInfo(null, SolveResult.NO_SOLUTION);
} else if (solutionCount[0] > 1) {
return new SolveInfo(null, SolveResult.MULTIPLE_SOLUTIONS);
} else {
return new SolveInfo(firstSolution, SolveResult.SOLVED);
}
}
/**
* 回溯算法核心实现(扩展版)
*/
private static void backtrackWithInfo(int[] candidates, int[] solution,
int[] solutionCounter, int[] firstSolution,
boolean hasFirstSolution) {
// 寻找候选数最少的空格
int index = -1;
int minCandidates = 10;
for (int i = 0; i < 81; i++) {
if (solution[i] == 0) {
int count = countBits(candidates[i]);
if (count < minCandidates) {
minCandidates = count;
index = i;
}
}
}
// 如果没有空格,说明已经解决
if (index == -1) {
solutionCounter[0]++;
if (solutionCounter[0] == 1) {
System.arraycopy(solution, 0, firstSolution, 0, 81);
}
return;
}
// 尝试该位置的每个候选值
int candidateValues = candidates[index];
for (int digit = 1; digit <= 9; digit++) {
if ((candidateValues & (1 << (digit - 1))) != 0) {
// 创建新的状态副本
int[] newCandidates = candidates.clone();
int[] newSolution = solution.clone();
// 设置当前数字
newSolution[index] = digit;
newCandidates[index] = 1 << (digit - 1);
// 传播约束
if (applyConstraints(newCandidates, newSolution, index, digit)) {
// 设置唯一候选数
if (setSingles(newCandidates, newSolution)) {
backtrackWithInfo(newCandidates, newSolution, solutionCounter, firstSolution, hasFirstSolution);
// 如果已经发现多解,提前结束
if (solutionCounter[0] > 1) {
return;
}
}
}
}
}
}
/**
* 应用约束传播
*/
private static boolean applyConstraints(int[] candidates, int[] solution, int index, int digit) {
int row = index / 9;
int col = index % 9;
int box = (row / 3) * 3 + (col / 3);
int mask = ~(1 << (digit - 1));
// 移除同行的候选数
for (int i = 0; i < 9; i++) {
int cellIndex = row * 9 + i;
if (cellIndex != index) {
candidates[cellIndex] &= mask;
}
}
// 移除同列的候选数
for (int i = 0; i < 9; i++) {
int cellIndex = i * 9 + col;
if (cellIndex != index) {
candidates[cellIndex] &= mask;
}
}
// 移除同宫的候选数
int boxRow = (box / 3) * 3;
int boxCol = (box % 3) * 3;
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
int cellIndex = (boxRow + i) * 9 + (boxCol + j);
if (cellIndex != index) {
candidates[cellIndex] &= mask;
}
}
}
// 检查是否有位置没有候选数且未填充
for (int i = 0; i < 81; i++) {
if (solution[i] == 0 && candidates[i] == 0) {
return false;
}
}
return true;
}
/**
* 设置所有唯一候选数(显性和隐性)
*/
private static boolean setSingles(int[] candidates, int[] solution) {
boolean changed;
do {
changed = false;
// 设置显性唯一候选数(Naked Singles)
for (int i = 0; i < 81; i++) {
if (solution[i] == 0 && countBits(candidates[i]) == 1) {
int digit = 1;
int temp = candidates[i];
while ((temp & 1) == 0) {
digit++;
temp >>= 1;
}
solution[i] = digit;
changed = true;
if (!applyConstraints(candidates, solution, i, digit)) {
return false;
}
}
}
// 检查行、列和宫中的隐性唯一候选数(Hidden Singles)
for (int digit = 1; digit <= 9; digit++) {
int mask = 1 << (digit - 1);
// 检查每行
for (int row = 0; row < 9; row++) {
int possiblePos = -1;
int count = 0;
for (int col = 0; col < 9; col++) {
int index = row * 9 + col;
if (solution[index] == 0 && (candidates[index] & mask) != 0) {
possiblePos = index;
count++;
}
}
if (count == 1) {
solution[possiblePos] = digit;
candidates[possiblePos] = mask;
changed = true;
if (!applyConstraints(candidates, solution, possiblePos, digit)) {
return false;
}
}
}
// 检查每列
for (int col = 0; col < 9; col++) {
int possiblePos = -1;
int count = 0;
for (int row = 0; row < 9; row++) {
int index = row * 9 + col;
if (solution[index] == 0 && (candidates[index] & mask) != 0) {
possiblePos = index;
count++;
}
}
if (count == 1) {
solution[possiblePos] = digit;
candidates[possiblePos] = mask;
changed = true;
if (!applyConstraints(candidates, solution, possiblePos, digit)) {
return false;
}
}
}
// 检查每个宫
for (int box = 0; box < 9; box++) {
int possiblePos = -1;
int count = 0;
int boxRow = (box / 3) * 3;
int boxCol = (box % 3) * 3;
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
int index = (boxRow + i) * 9 + (boxCol + j);
if (solution[index] == 0 && (candidates[index] & mask) != 0) {
possiblePos = index;
count++;
}
}
}
if (count == 1) {
solution[possiblePos] = digit;
candidates[possiblePos] = mask;
changed = true;
if (!applyConstraints(candidates, solution, possiblePos, digit)) {
return false;
}
}
}
}
} while (changed);
return true;
}
/**
* 计算位整数中1的位数
*/
private static int countBits(int n) {
int count = 0;
while (n > 0) {
count += n & 1;
n >>= 1;
}
return count;
}
}
许可协议:
转载标注作者